数学与统计学院王锦荣教授课题组指导的2019级博士研究生刘蕊在国际模糊数学与模糊系统领域顶级杂志Fuzzy Sets and Systems(一区,IF=2.907)连续发表2篇高水平论文:
[1] On the solutions of first-order linear impulsive fuzzy differential equations,(2019), https://doi.org/10.1016/j.fss.2019.11.001
[2] Ulam type stability of first-order linear impulsive fuzzy differential equations,(2019), https://doi.org/10.1016/j.fss.2019.10.007
模糊微分方程是模糊数学的重要分支,也是当今研究热点问题之一。文献[1,2]是在课题组前期对非模糊线性脉冲系统研究的基础上开展的连续研究,分别对一阶线性脉冲模糊微分方程的解和对其Ulam型稳定性进行了系统完整研究。
文献[1]给出了一阶常系数线性脉冲模糊微分方程的解的表示。利用广义可微性概念和脉冲基本矩阵,提出了与脉冲模糊柯西问题线性模糊微分方程相似的思想。本文将模糊微分方程转化为带有上下分支的常微分方程,进而在常微分理论的基础上进行求解。该工作是研究脉冲模糊微分方程奠基性工作,具有里程碑式的意义。
对于一阶线性微分方程(在非模糊环境下),方程的形式和系数的符号都不影响其解。然而,在模糊环境下,情况就更加复杂。在前人的研究工作中给出了模糊环境下非脉冲情况的Ulam型稳定性的叙述,但是非脉冲情况在实际应用还是有局限性。基于上述发现,文献[2]首次提出了一阶线性脉冲模糊微分方程Ulam型稳定性概念的叙述,并且分别讨论了以下三种情形Ulam型稳定性存在的充分条件:
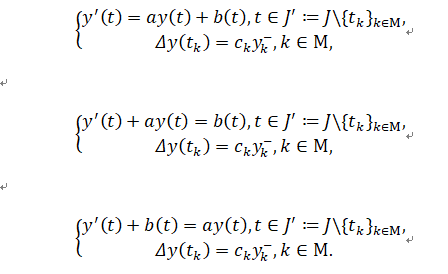
上述研究成果为后续从事脉冲模糊微分方程控制问题夯实了必须的理论基础,同时也为包括工程,生物,医学在内的众多领域的技术发展提供了必要的理论依据。

